In Part 1 of this series, I introduced my newest project: Late, the Language Agnostic Templating Engine. This is my first real foray into compilers and interpreters, often the most complex and esoteric aspects of Computer Science, and I’m documenting what I learn as I go. Today, we will cover the three main aspects of most any language: lexing, parsing, and compilation/evaluation.

When it comes to building your own language, one can easily get overwhelmed by the sheer quantity of research papers, blog posts, and tools that exist today. Should you use lex, flex, bison, or yacc? Or what about things like ANTLR? And where does LLVM fit into all of this? And if you happen to run into descriptions of AST rewriting, optimization passes, SSA, and tools like a Just-In-Time compilation, it can be enough for anyone to just say “Nope! This is all over my head” and move on. The trick is to start with one piece at a time. At its core, compilation is a pipeline, where each step has explicitly defined inputs and outputs. To understand how languages are built we go one step at a time and eventually the whole picture suddenly makes sense!

Now it would be rude of me to not give credit where credit is due. The only reason I’ve been able to dive into Late and the entire world of templating languages like this is because I found and read Thorsten Ball’s fantastic book “Writing an Interpreter In Go.” In this book, Thorsten does a great job of distilling the magic of interpreters into simple, well explained, and understandable pieces. By the end, you end up with a working and quite capable interpreted language. These posts, and Late itself, probably wouldn’t exist without this book, so thanks Thorsten!

Almost every language out there is designed around three main phases:

• Tokenization and lexicographical analysis (often called lexing)
• Applying meaning to the resulting tokens (parsing)
• Compiling and/or evaluating the results of the parser

It sounds like a lot, but as I said earlier, we are going to take this one step at a time. If you would prefer a more hands-on example, please go grab Thorsten’s book!

Tokenizing and Lexing

First up is the Lexer. While this is technically two pieces (tokenizing and lexicographical analysis), almost every language combines the two into one step. The Lexer takes the source input (the template, the scripting language file, etc) and splits it into tokens, often with accompanying metadata like line numbers and raw input. These tokens are intended to be mostly context free, but meaningful to the language.

As an example, say you have the following source code

a = b * 2

Lexing this will provide a list of tokens much like:

IDENTIFIER("a")
OPERAND("=")
IDENTIFIER("b")
OPERAND("*")
INTEGER(2)

For a more complex example, say you were lexing the following Ruby-esque code.

def add(x, y)
  x + y
end

The lexer result will look something like this:

KEYWORD("def")
IDENTIFIER("add")
LPAREN("(")
IDENTIFIER("x")
COMMA(",")
IDENTIFIER("y")
RPAREN(")")
IDENTIFIER("x")
OPERAND("+")
IDENTIFIER("y")
KEYWORD("end")

It’s important to note here that the tokens are very generic, providing only the most basic information about each token. It’s not the lexer’s job to determine if the syntax is correct, and in many cases the only errors a lexer will throw is if it finds a character it doesn’t know how to handle, or an unexpected EOF marker when tokenizing things like strings.

While lexers for most programming languages are stateless, reading through the input and processing every character, templating engines like Late need a little bit of state to work properly. Templating engines expect the templating code itself to be secondary to the main content of the input. As such, the lexer should happily accept anything up until the point of reaching an “open code” token (in Liquid and Late that would be {{ or {%). However, we do need to keep around the non-Late code for generation of the final file, so all non-Late code gets tokenized into special RAW tokens.

You can see how this is implemented in Late’s template/lexer package. With our list of tokens now done, it’s time to move onto the parser and give these tokens meaning.

Parsing and ASTs

Parsing is where we take the list of tokens from the lexer and build a structure that gives actionable meaning to the input. For most languages, including Late, the structure we build is called an Abstract Syntax Tree, or AST. Using a tree structure (specifically a binary tree, where each node has at most two children) is powerful because it lets us encode not only order-of-operation, but also operator precedence in the same structure (ensuring that 2 + 3 * 5 is 17 and not 25). Also, tree structures are trivial to iterate through using well known algorithms, making the evaluation step easy to implement.

Parsing is a huge topic and one that has received many decades worth of research. I recently ran into a detailed history of parsing timeline that may give you an idea of the depth and breadth of this topic. There is far too much to try to cover in a single blog post, so today I’m going to go over how Late’s parser works at a high level. You can see the full details in parser.go. There’s a lot here so we’ll take it step-by-step.

Building up a parser to handle complex languages can seem like a sizable task, but like everything else with compilers, we can start at the simplest possible point and build up complexity from there. We start with two definitions: Expression and Statement. Expressions result in values (such as 1, "this", and 1 + 2) while Statements are, in Late’s case, how we keep track of raw input: variables ({{ }}) and tags ({% %}). With this, we start with parsing literal expressions (ones that evaluate to themselves): strings, numbers, identifiers, and booleans. When the parser sees these tokens from the lexer, it applies a one-to-one mapping from the lexer token to the appropriate AST node. See parseIdentifier, parseNumberLiteral, parseStringLiteral, and parseBooleanLiteral for the details.

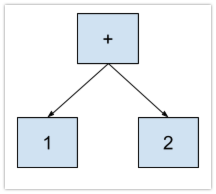
We can now move onto simple compound expressions like 1 + 2. It’s important to view this code snippet not as “number + number” but “expression operator expression”. This is where recursion comes into play and is why this type of parser is called Recursive Decent. To handle this code, we step through the tokens, parsing expressions as we see them and finishing by linking them together with the operator. Through that we end up with an AST that looks like:

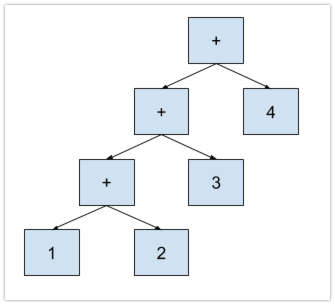
Once we have this this working, expanding to parse other expressions gets easier. For example, take 1 + 2 + 3 + 4. You may wonder if the parser needs to have cases to handle up to a certain number of chained operators. Thankfully this is not required, as every operator expression can be represented in a [left expression]-[operator]-[right expression] tree format. To do this, we take the expression one operator at a time: 1 + 2, then add + 3, and then + 4. In explicit grouping, the expression looks like this (((1 + 2) + 3) + 4) to the parser giving us the following AST:

Now, this gets a little more complicated when it comes to operator precedence. With a pure left-to-right parser, the statement 1 + 2 * 3 will parse and evaluate to be 9 (e.g. (1 + 2) * 3), vs applying the rules of mathematics and operator precedence, in which the right answer is 7 (e.g. 1 + (2 * 3)). There are many algorithms available to handle operator precedence and it is the source of much of the research into parsers. Late, through the recommendation in Thorsten’s book, uses a Pratt parser to handle this. While this type of parser is much easier to explain and implement than many others, it’s still too much to cover here. I’ll go into more detail in the next blog post, but for now here’s the core of a Pratt parser:

• Each operator is given a precedence level, where a higher number means greater precedence (e.g. * > +)
• Each input token is linked to a “prefix” function (-a), an “infix” function (1 + 2), or both ([ in definition [1,2,3] and access array[1]).
• Parsing starts at a given precedence, normally the lowest possible, and iterates through tokens until it finds the end of the expression or a token with a lower precedence than the current.

These three rules make for a surprisingly simple yet powerful parser. The entire logic for this can be found in parseExpression, and I’ll go into more detail on how this all works in my next post.

With all of the above in place, parsing more complex expressions, especially heavily nested expressions like [1, 1 + 1, "three", [1, 2, 3, "four"][3]] becomes automatic. The parser will see this input as nothing more than [expression, expression, expression, expression] and recursion takes care of the rest. You can see this happening in parseArrayLiteral, where we handle the empty case [], one element arrays [1], and then many element arrays in about 15 lines of code.

The parser runs through the whole list of tokens, building ASTs for each Late section. It’s now time to evaluate these trees and return the results!

Compiling and Evaluation

The third step of the toolchain is one that can range from almost trivial (iterating through and evaluating an AST) to complex (generating optimized machine code for the fastest execution possible), but just like the rest of this article, learning how to process the ASTs generated by the parser begins with the simplest steps. Whether you’re working on a templating language evaluator, a language interpreter (like Ruby pre 1.9), or compiling all the way to machine code, it’s important to start as simple and small as possible. The complexity will come naturally as long as you focus on building small, simple steps towards your goal. Remember, LLVM didn’t just instantly appear as the behemoth it is today. LLVM has been in development for over fifteen years (the first white paper was published in 2002) and even then was already building on decades of compiler research and knowledge that came before it.

With Late, and most templating languages, we aren’t building a full-fledged programming language which affords us a lot of leeway in how we implement this last step. Also as templating is a one-pass evaluation tool, execution speed isn’t a super high priority, so focusing on the simplest and most readable implementation is a great way to start. As such, Late’s evaluator runs through each AST with a depth-first algorithm, making use of a large switch statement to know how to handle each type of AST node. You can see this in the eval function in evaluator.go. Depth-first means we iterate through the tree, moving onto children nodes and evaluating from the absolute bottom of the tree first. Those results then propogate back up the tree and when we are back at the root of the tree, we know evaluation for that tree is done. Here’s a visual of how this works for 1 + 2 + 3 + 4:

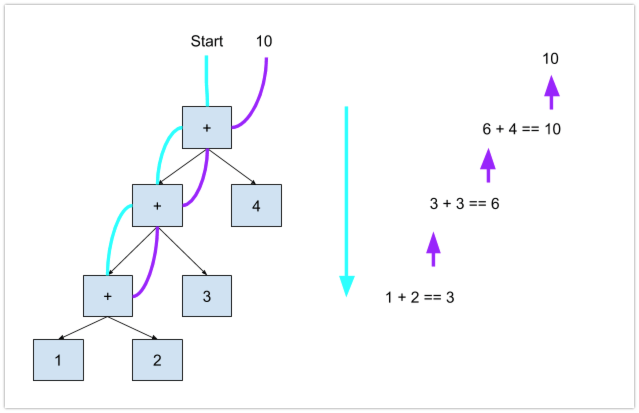
Once every tree has been evaluated, the results are then concatenated back into a single string and returned as the output document. This logic can be found in template.go, which ties the whole process together.

The last piece required to understand Late’s evaluation is how it handles the values and data that users will want to use and expose in their templates. Late has a simple, dynamically-typed data model, where a variable can hold any data type and an array can contain any mix of variables, e.g. [1, "two", [3]]). This data model is implemented in Late’s object package, where you can see how Late maps built-in Go types into and out of a dynamic wrapper.

And that’s the basic run-down of how Late works! There’s a lot here and it can seem overhelming, but as long as you take each piece on its own, and only move on to the next once you’re comfortable, understanding the full system is possible. Hopefully this has provided enough guidance to not only help understand Late’s code, but also to whet your appetite for learning how other languages work, or even writing your own!

In my next post I’ll be doing a deep dive into the Pratt parser algorithm, because this thing is slick and a great example of how simple rules can solve complex problems.